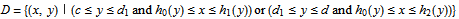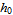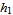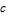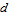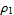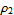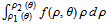Élément différentiel dA
Integration over the region in the plane between the graphs of two continuous functions is performed by setting up type I or type II domains in Cartesian coordinates or as a polar domain in polar coordinates. Double integrals require a student to visualize the differential element of area covering the desired domain of integration. Using an integrand function of value 1 everywhere generates a double integral whose value is the area of the domain.
A plane region 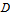 is type I if it lies between the graphs of two continuous functions
is type I if it lies between the graphs of two continuous functions  and
and  of
of 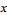 on [
on [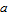 ,
,  ], that is,
], that is, 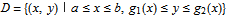 . Vertical strips
. Vertical strips 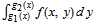 are integrated as
are integrated as 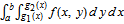 shown by "x strip history" control.
shown by "x strip history" control.
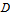 is type I if it lies between the graphs of two continuous functions
is type I if it lies between the graphs of two continuous functions 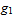 and
and  of
of 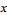 on [
on [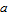 ,
,  ], that is,
], that is, 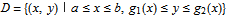 . Vertical strips
. Vertical strips 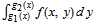 are integrated as
are integrated as 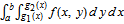 shown by "x strip history" control.
shown by "x strip history" control.A plane region 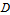 is type II if it lies between the graphs of two continuous functions
is type II if it lies between the graphs of two continuous functions 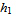 and
and 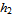 of
of 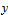 on [
on [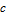 ,
, 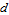 ], that is,
], that is,
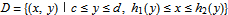 . Horizontal strips
. Horizontal strips  are integrated as
are integrated as 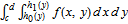 shown by "y strip history" control.
shown by "y strip history" control.
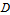 is type II if it lies between the graphs of two continuous functions
is type II if it lies between the graphs of two continuous functions 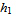 and
and 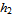 of
of 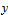 on [
on [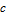 ,
, 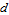 ], that is,
], that is, 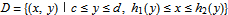 . Horizontal strips
. Horizontal strips  are integrated as
are integrated as 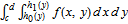 shown by "y strip history" control.
shown by "y strip history" control.Differential Element dA from the Wolfram Demonstrations Project by Harry Bishop
Modifié le: mardi 7 mai 2013, 22:17